Метод штрафных функций

Методы штрафных функций или методы штрафов (Penalty method) — методы, широко используемые для решения технических задач оптимизации. Эффективны если штрафная функция естественно вытекает из технического смысла задачи. ©Википедия
Впрочем гуглить думаю вы и сами умеете, я же в этом посте хочу выложить исходники своего курсового с 3его курса, а именно реализацию метода штрафных функций. Язык C#.
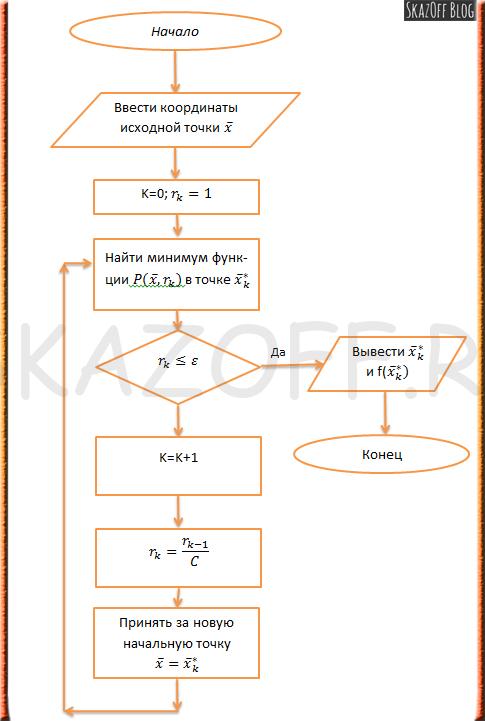
Алгоритм можно почитать вот тут. В моей ПЗ к курсовому была вот такая блок-схема (как же я их не любил рисовать >_<).
И в итоге получилась вот такая вот програмулина
А теперь как это все получилось. Внимание дальше будет сплошной код! 😉
Для построения графика
using ZedGraph;
Объявляем основные коэффициенты
// коэффициенты условий
double n1_1, n1_2,n1_3, n2_1, n2_2,n2_3, n3_1, n3_2, n3_3, n4_1, n4_2;
// дополнительные перемменные
double r, C, x01, x02,Eps,Eps_main;
//коэффициетты у функции
double fk1, fk2,fk3,fk4;
Далее считываем все данные для коэффициентов и переводим их в Double, например так
fk2 = Convert.ToDouble(textBox13.Text);
поскольку их очень много весь код писать не буду, для каждого коэффициента он одинаков.
Все производные от основной функции
// значение производной по х1 от функции в указанной точке
double fp_x1(double x1, double x2) { return 2 * x1 - 2 * fk1+x2-fk4; }
// значение второй производной по х1 от функции (первая производная взята по х1)в указанной точке
double fp_x1_x1(double x1, double x2) { return 2; }
// значение второй производной по х2 от функции (первая производная взята по х1)в указанной точке
double fp_x1_x2(double x1, double x2) { return 1; }
// значение производной по х2 от функции в указанной точке
double fp_x2(double x1, double x2) { return 2 * x2 - 2 * fk2 +x1-fk3; }
// значение второй производной по х1 от функции (первая производная взята по х2)в указанной точке
double fp_x2_x1(double x1, double x2) { return 1; }
// значение второй производной по х2 от функции (первая производная взята по х2)в указанной точке
double fp_x2_x2(double x1, double x2) { return 2; }
// значение производной по х1 от условия в указанной точке (для одного условия) все условия приведены к типу ax1+bx2+c>=0
double rp_x1(double a, double b, double c, double x1, double x2) {
if (a == 0 && b == 0)
return 0;
double d = a * x1 + b * x2 + c;
return -a / (d*d); }
// значение производной по х2 от условия в указанной точке (для одного условия)
double rp_x2(double a, double b, double c, double x1, double x2) {
if (a == 0 && b == 0)
return 0;
double d = a * x1 + b * x2 + c;
return -b / (d * d); }
// значение второй производной по х1 от условия (первая производная взята по х1)в указанной точке
double rp_x1_x1(double a, double b, double c, double x1, double x2) {
if (a == 0 && b == 0)
return 0;
double d = a * x1 + b * x2 + c;
double e = 2 * a * a * x1 + 2 * a * b * x2 + 2 * a * c;
return (a * e) / (d * d * d * d); }
// значение второй производной по х1 от условия (первая производная взята по х2)в указанной точке
double rp_x2_x1(double a, double b, double c, double x1, double x2) {
if (a == 0 && b == 0)
return 0;
double d = a * x1 + b * x2 + c;
double e = 2 * a * a * x1 + 2 * a * b * x2 + 2 * a * c;
return (b * e) / (d * d * d * d); }
// значение второй производной по х2 от условия (первая производная взята по х1)в указанной точке
double rp_x1_x2(double a, double b, double c, double x1, double x2) {
if (a == 0 && b == 0)
return 0;
double d = a * x1 + b * x2 + c;
double e = 2 * b * b * x2 + 2 * a * b * x1 + 2 * b * c;
return (a * e) / (d * d * d * d); }
// значение второй производной по х2 от условия (первая производная взята по х2)в указанной точке
double rp_x2_x2(double a, double b, double c, double x1, double x2) {
if (a == 0 && b == 0)
return 0;
double d = a * x1 + b * x2 + c;
double e = 2 * b * b * x2 + 2 * a * b * x1 + 2 * b * c;
return (b * e) / (d * d * d * d); }
//значение функции F в указанной точке
double f(double x1, double x2) { return (x1-fk1)*(x1-fk1)+(x2-fk2)*(x2-fk2)+(x1-fk3)*(x2-fk4); }
//значение условия F в указанной точке
double rf(double a, double b, double c, double x1, double x2) {
if (a == 0 && b == 0)
return 0;
return 1/(a*x1+b*x2+c); }
//значение всей общей функции F= f+r*(cсумма(условий)) в указанной точке
double F_main(double x1, double x2) {
return f(x1, x2) + r * (rf(n1_1, n1_2, n1_3, x1, x2) + rf(n2_1, n2_2, n2_3, x1, x2) + rf(n3_1, n3_2, n3_3, x1, x2) + rf(1, 0, n4_1, x1, x2) + rf(0, 1, n4_2, x1, x2)); }
Считаем значение градиентов
// значение градиента функции в указанной точке
double[] Gradient(double x1, double x2) {
double[] grad = { 0, 0 };
grad[0] = fp_x1(x1, x2) + r * (rp_x1(n1_1, n1_2, n1_3, x1, x2) + rp_x1(n2_1, n2_2, n2_3, x1, x2) + rp_x1(n3_1, n3_2, n3_3, x1, x2) + rp_x1(1, 0, n4_1, x1, x2) + rp_x1(0, 1, n4_2, x1, x2));
grad[1] = fp_x2(x1, x2) + r * (rp_x2(n1_1, n1_2, n1_3, x1, x2) + rp_x2(n2_1, n2_2, n2_3, x1, x2) + rp_x2(n3_1, n3_2, n3_3, x1, x2) + rp_x2(1, 0, n4_1, x1, x2) + rp_x2(0, 1, n4_2, x1, x2));
return grad; }
// значение градиента2 функции в указанной точке
double[,] Gradient2(double x1, double x2) {
double[,] grad = new double[2, 2];
grad[0, 0] = fp_x1_x1(x1, x2) + r * (rp_x1_x1(n1_1, n1_2, n1_3, x1, x2) + rp_x1_x1(n2_1, n2_2, n2_3, x1, x2) + rp_x1_x1(n3_1, n3_2, n3_3, x1, x2) + rp_x1_x1(1, 0, n4_1, x1, x2) + rp_x1_x1(0, 1, n4_2, x1, x2));
grad[0, 1] = fp_x1_x2(x1, x2) + r * (rp_x1_x2(n1_1, n1_2, n1_3, x1, x2) + rp_x1_x2(n2_1, n2_2, n2_3, x1, x2) + rp_x1_x2(n3_1, n3_2, n3_3, x1, x2) + rp_x1_x2(1, 0, n4_1, x1, x2) + rp_x1_x2(0, 1, n4_2, x1, x2));
grad[1, 0] = fp_x2_x1(x1, x2) + r * (rp_x2_x1(n1_1, n1_2, n1_3, x1, x2) + rp_x2_x1(n2_1, n2_2, n2_3, x1, x2) + rp_x2_x1(n3_1, n3_2, n3_3, x1, x2) + rp_x2_x1(1, 0, n4_1, x1, x2) + rp_x2_x1(0, 1, n4_2, x1, x2));
grad[1, 1] = fp_x2_x2(x1, x2) + r * (rp_x2_x2(n1_1, n1_2, n1_3, x1, x2) + rp_x2_x2(n2_1, n2_2, n2_3, x1, x2) + rp_x2_x2(n3_1, n3_2, n3_3, x1, x2) + rp_x2_x2(1, 0, n4_1, x1, x2) + rp_x2_x2(0, 1, n4_2, x1, x2));
return grad; }
И ищем минимум функции с помощью метода Ньютона
double[] Nyton(double x1, double x2) {
double[] rez = { 0, 0 };
while (true) {
double[,] obr_gradient = obr(Gradient2(x1, x2));
double[] grad = Gradient(x1, x2);
rez[0] = x1 - obr_gradient[0, 0] * grad[0] - obr_gradient[0, 1] * grad[1];
rez[1] = x2 - obr_gradient[1, 0] * grad[0] - obr_gradient[1, 1] * grad[1];
if (rez[0] - x1 < Eps && rez[1] - x2 < Eps)
return rez;
else {
x1 = rez[0];
x2 = rez[1]; }
}
}
Нахождение обратной матрицы
double[,] obr(double[,] A)
{
int n = A.GetLength(0);
double[,] rez = new double[n, n];
double[,] temp = new double[n, n];
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
temp[i, j] = A[i, j];
}
}
double determ = det(temp);
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
rez[i, j] = alg(A, i, j);
rez[i, j] /= determ;
}
}
return rez;
}
Находим алгебраические дополнения
double alg(double[,] A, int ii, int jj)
{
int n = A.GetLength(0);
double[,] B = new double[n, n];
double[,] C = new double[n - 1, n - 1];
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
B[i, j] = A[i, j];
}
}
for (int i = jj + 1; i < n; i++)
{
for (int j = 0; j < n; j++)
{
B[i - 1, j] = A[i, j];
}
}
for (int i = ii + 1; i < n; i++)
{
for (int j = 0; j < n; j++)
{
B[j, i - 1] = B[j, i];
}
}
for (int i = 0; i < n - 1; i++)
{
for (int j = 0; j < n - 1; j++)
{
C[i, j] = B[i, j];
}
}
return Math.Pow((-1), (ii + jj + 2)) * det(C);
}
Ищем определитель матрицы
double det(double[,] A)
{
int zamena = 0;
int n = A.GetLength(0);
double det = 1, temp, temp1;
for (int k = 0; k < n; k++)
{
if (A[k, k] == 0)
{
zamena += 1;
for (int i = k; i < n; i++)
{
if (A[i, k] != 0)
{
for (int j = 0; j < n; j++)
{
temp = A[i, j];
A[i, j] = A[k, j];
A[k, j] = temp;
}
break;
}
}
}
temp1 = A[k, k];
for (int i = 0; i < n; i++)
{
temp = A[i, k] / temp1;
if (i != k)
{
for (int j = 0; j < n; j++)
{
A[i, j] = A[i, j] - A[k, j] * temp;
}
}
}
}
for (int i = 0; i < n; i++)
det = det * A[i, i];
return Math.Pow(-1, zamena) * det;
}
Главная функция
void main() {
// Получим панель для рисования
GraphPane pane = zedGraph.GraphPane;
// Очистим список кривых на тот случай, если до этого сигналы уже были нарисованы
pane.CurveList.Clear();
// Создадим список точек
PointPairList list = new PointPairList();
// PointPairList list_my = new PointPairList();
pane.XAxis.Title.Text = "Итерации";
pane.YAxis.Title.Text = "Значение функции";
pane.Title.Text = "";
// Заполняем список точек
double x1 = x01;
double x2 = x02;
double F0 = 0, F1 = 0;
double iter = 0;
F0 = f(x1, x2);
textBox21.Text = F0.ToString();
list.Add(iter, F0);
bool exit = false;
// сам метод штрафных функций
while (!exit)
{
iter += 1;
double[] rez=Nyton(x1, x2);
x1 = rez[0];
x2 = rez[1];
F1 = f(x1, x2);
list.Add(iter, F1);
if (Math.Abs(F1 - F0) < Eps_main)
exit = true;
r = r / C;
textBox21.Text +="\r\n" +F1.ToString();
F0 = F1;
}
textBox20.Text = F0.ToString();
// Создадим кривую с названием "Sinc",
// которая будет рисоваться голубым цветом (Color.Blue),
// Опорные точке выделяться не будут (SymbolType.None)
LineItem myCurve = pane.AddCurve("F(x,r)", list, Color.Blue, SymbolType.Triangle);
// Вызываем метод AxisChange (), чтобы обновить данные об осях.
// В противном случае на рисунке будет показана только часть графика,
// которая умещается в интервалы по осям, установленные по умолчанию
zedGraph.AxisChange();
// Обновляем график
zedGraph.Invalidate();
}
Вот на этом все. Всего скорее это можно было сделать и без таких заморочек, но как сделано так сделано 🙂
Добавить комментарий